Knowledge Base
Vibrations
The fundamentals of vibration analysis can be understood by studying the simple mass–spring–damper model. Indeed, even a complex structure such as an automobile body can be modeled as a "summation" of simple mass–spring–damper models. The mass–spring–damper model is an example of a simple harmonic oscillator. The mathematics used to describe its behavior is identical to other simple harmonic oscillators such as the RLC circuit.
Free vibration without damping
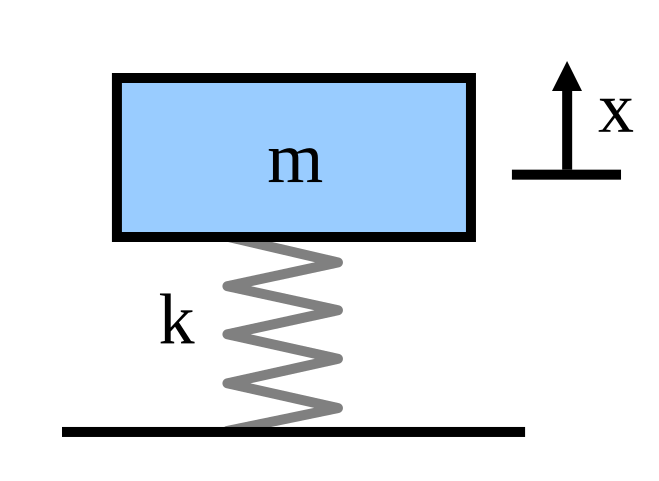
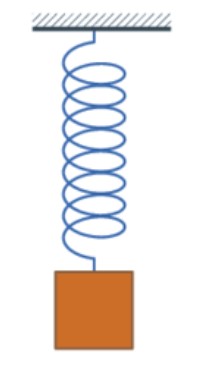
To start the investigation of the mass–spring–damper we will assume the damping is negligible and that there is no external force applied to the mass (i.e. free vibration).
The force applied to the mass by the spring is proportional to the amount the spring is stretched "x" (we will assume the spring is already compressed due to the weight of the mass). The proportionality constant, k, is the stiffness of the spring and has units of force/distance (e.g. lbf/in or N/m)
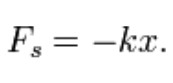
The force generated by the mass is proportional to the acceleration of the mass as given by Newton’s second law of motion.
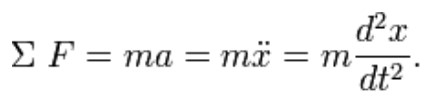
The sum of the forces on the mass then generates this ordinary differential equation:
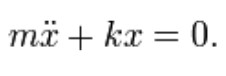
Simple harmonic motion of the mass–spring system
If we assume that we start the system to vibrate by stretching the spring by the distance of A and letting go, the solution to the above equation that describes the motion of mass is:
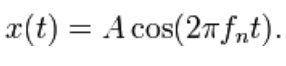
This solution says that it will oscillate with simple harmonic motion that has an amplitude of A and a frequency of fn. The number fn is one of the most important quantities in vibration analysis and is called the undamped natural frequency. For the simple mass–spring system, fn is defined as:
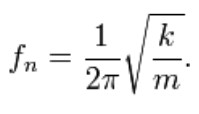
Note: Angular frequency ω
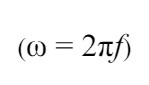
with the units of radians per second is often used in equations because it simplifies the equations, but is normally converted to “standard” frequency (units of Hz or equivalently cycles per second) when stating the frequency of a system.
If you know the mass and stiffness of the system you can determine the frequency at which the system will vibrate once it is set in motion by an initial disturbance using the above stated formula. Every vibrating system has one or more natural frequencies that it will vibrate at once it is disturbed. This simple relation can be used to understand in general what will happen to a more complex system once we add mass or stiffness. For example, the above formula explains why when a car or truck is fully loaded the suspension will feel “softer” than unloaded because the mass has increased and therefore reduced the natural frequency of the system.
What causes the system to vibrate: from conservation of energy point of view
Vibrational motion could be understood in terms of conservation of energy.
In the above example we have extended the spring by a value of x and therefore have stored some potential energy (1/2 kx2) in the spring. Once we let go of the spring, the spring tries to return to its un-stretched state (which is the minimum potential energy state) and in the process accelerates the mass. At the point where the spring has reached its un-stretched state all the potential energy that we supplied by stretching it has been transformed into kinetic energy (1/2 mv2). The mass then begins to decelerate because it is now compressing the spring and in the process transferring the kinetic energy back to its potential. Thus oscillation of the spring amounts to the transferring back and forth of the kinetic energy into potential energy.
In our simple model the mass will continue to oscillate forever at the same magnitude, but in a real system there is always something called damping that dissipates the energy and therefore the system eventually bringing it to rest.
Free vibration with damping
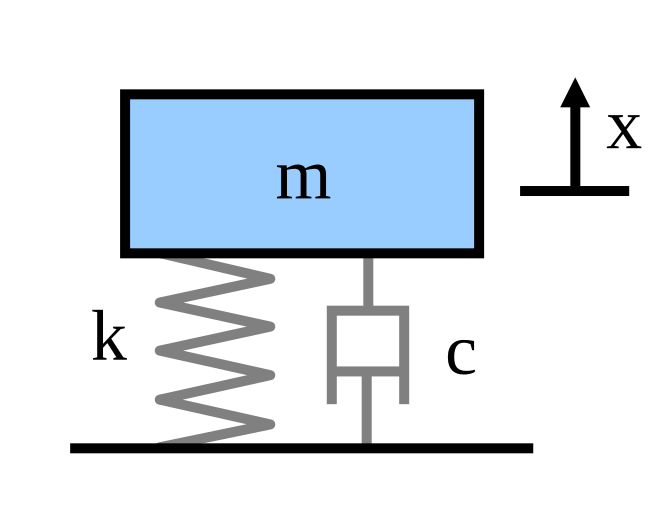
We now add a "viscous" damper to the model that outputs a force that is proportional to the velocity of the mass. The damping is called viscous because it models the effects of an object within a fluid. The proportionality constant c is called the damping coefficient and has units of Force over velocity (lbf s/ in or N s/m).
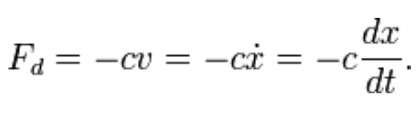
By summing the forces on the mass we get the following ordinary differential equation:
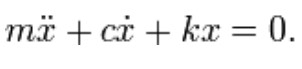
The solution to this equation depends on the amount of damping. If the damping is small enough the system will still vibrate, but eventually, over time, will stop vibrating. This case is called underdamping – this case is of most interest in vibration analysis. If we increase the damping just to the point where the system no longer oscillates we reach the point of critical damping (if the damping is increased past critical damping the system is called over damped). The value that the damping coefficient needs to reach for critical damping in the mass spring damper model is:
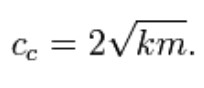
To characterize the amount of damping in a system a ratio called the damping ratio (also known as damping factor and % critical damping) is used. This damping ratio is just a ratio of the actual damping over the amount of damping required to reach critical damping. The formula for the damping ratio (ζ) of the mass spring damper model is:
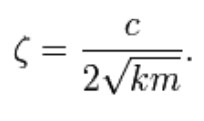
For example, metal structures (e.g. airplane fuselage, engine crankshaft) will have damping factors less than 0.05 while automotive suspensions in the range of 0.2–0.3.
The solution to the under damped system for the mass spring damper model is the following:
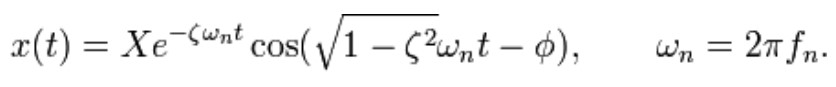
The value of X, the initial magnitude, and φ, the phase shift, are determined by the amount the spring is stretched. The formulas for these values can be found in the references
Damped and undamped natural frequencies
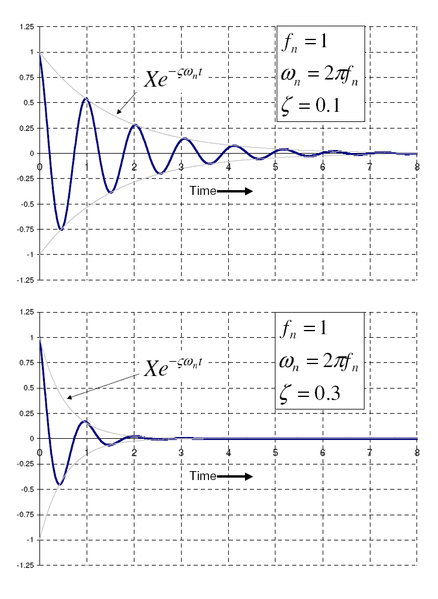
The major points to note from the solution are the exponential term and the cosine function. The exponential term defines how quickly the system “damps” down – the larger the damping ratio, the quicker it damps to zero. The cosine function is the oscillating portion of the solution, but the frequency of the oscillations is different from the undamped case.
The frequency in this case is called the "damped natural frequency", ƒd, and is related to the undamped natural frequency by the following formula:
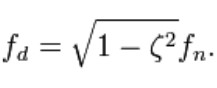
The damped natural frequency is less than the undamped natural frequency, but for many practical cases the damping ratio is relatively small and hence the difference is negligible. Therefore the damped and undamped description are often dropped when stating the natural frequency (e.g. with 0.1 damping ratio, the damped natural frequency is only 1% less than the undamped).
The plots to the side present how 0.1 and 0.3 damping ratios effect how the system will “ring” down over time. What is often done in practice is to experimentally measure the free vibration after an impact (for example by a hammer) and then determine the natural frequency of the system by measuring the rate of oscillation as well as the damping ratio by measuring the rate of decay. The natural frequency and damping ratio are not only important in free vibration, but also characterize how a system will behave under forced vibration.
Forced vibration with damping
In this section we will see the behavior of the spring mass damper model when we add a harmonic force in the form below. A force of this type could, for example, be generated by a rotating imbalance.
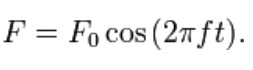
If we again sum the forces on the mass we get the following ordinary differential equation:
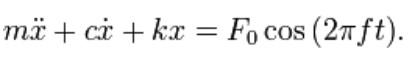
The steady state solution of this problem can be written as:
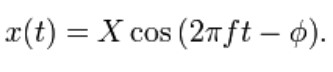
The result states that the mass will oscillate at the same frequency, f, of the applied force, but with a phase shift φ.
The amplitude of the vibration “X” is defined by the following formula.
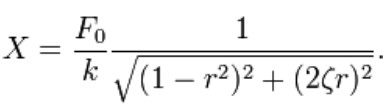
Where “r” is defined as the ratio of the harmonic force frequency over the undamped natural frequency of the mass–spring–damper model.
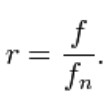
The phase shift , φ, is defined by the following formula.
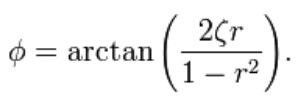
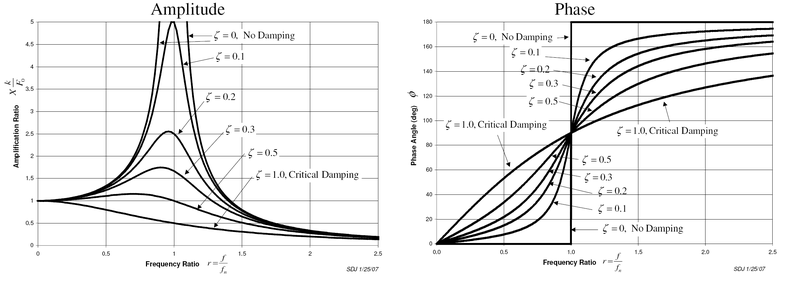
The plot of these functions, called "the frequency response of the system", presents one of the most important features in forced vibration. In a lightly damped system when the forcing frequency nears the natural frequency (r≈1) the amplitude of the vibration can get extremely high. This phenomenon is called resonance (subsequently the natural frequency of a system is often referred to as the resonant frequency). In rotor bearing systems any rotational speed that excites a resonant frequency is referred to as a critical speed.
If resonance occurs in a mechanical system it can be very harmful – leading to eventual failure of the system. Consequently, one of the major reasons for vibration analysis is to predict when this type of resonance may occur and then to determine what steps to take to prevent it from occurring. As the amplitude plot shows, adding damping can significantly reduce the magnitude of the vibration. Also, the magnitude can be reduced if the natural frequency can be shifted away from the forcing frequency by changing the stiffness or mass of the system. If the system cannot be changed, perhaps the forcing frequency can be shifted (for example, changing the speed of the machine generating the force).
The following are some other points in regards to the forced vibration shown in the frequency response plots
- At a given frequency ratio, the amplitude of the vibration, X, is directly proportional to the amplitude of the force F0 (e.g. if you double the force, the vibration doubles)
- With little or no damping, the vibration is in phase with the forcing frequency when the frequency ratio r < 1 and 180 degrees out of phase when the frequency ratio r > 1
- When r ≪1 the amplitude is just the deflection of the spring under the static force F0. This deflection is called the static deflection δst. Hence, when r ≪1 the effects of the damper and the mass are minimal.
- When r ≫1 the amplitude of the vibration is actually less than the static deflection δst. In this region the force generated by the mass (F = ma) is dominating because the acceleration seen by the mass increases with the frequency. Since the deflection seen in the spring, X, is reduced in this region, the force transmitted by the spring (F = kx) to the base is reduced. Therefore the mass–spring–damper system is isolating the harmonic force from the mounting base – referred to as vibration isolation. Interestingly, more damping actually reduces the effects of vibration isolation when r ≫1 because the damping force (F = cv) is also transmitted to the base.
What causes resonance?
Resonance is simple to understand if you view the spring and mass as energy storage elements – with the mass storing kinetic energy and the spring storing potential energy. As discussed earlier, when the mass and spring have no force acting on them they transfer energy back and forth at a rate equal to the natural frequency. In other words, if energy is to be efficiently pumped into both the mass and spring the energy source needs to feed the energy in at a rate equal to the natural frequency. Applying a force to the mass and spring is similar to pushing a child on swing, you need to push at the correct moment if you want the swing to get higher and higher. As in the case of the swing, the force applied does not necessarily have to be high to get large motions; the pushes just need to keep adding energy into the system.
The damper, instead of storing energy, dissipates energy. Since the damping force is proportional to the velocity, the more the motion, the more the damper dissipates the energy. Therefore a point will come when the energy dissipated by the damper will equal the energy being fed in by the force. At this point, the system has reached its maximum amplitude and will continue to vibrate at this level as long as the force applied stays the same. If no damping exists, there is nothing to dissipate the energy and therefore theoretically the motion will continue to grow on into infinity.