Knowledge Base
Underwater Noise
Sound waves in water
A sound wave propagating underwater consists of alternating compressions and rarefactions of the water. These compressions and rarefactions are detected by a receiver, such as the human ear or a hydrophone, as changes in pressure. These waves may be man-made or naturally generated.
Speed of sound, density and impedance
The speed of sound c (i.e., the longitudinal motion of wave fronts) is related to frequency ƒ and wavelength ⋋ of a wave by
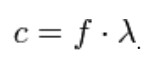
This is different from the particle velocity u, which refers to the motion of molecules in the medium due to the sound, and relates the plane wave the pressure p to the fluid density ρ and sound speed cby
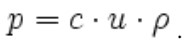
The product of c and ρ from the above formula is known as the characteristic acoustic impedance. The acoustic power (energy per second) crossing unit area is known as the intensity of the wave and for a plane wave the average intensity is given by
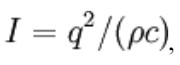
where is q the root mean square acoustic pressure
At 1 kHz, the wavelength is about 1.5 m. Sometimes the term "sound velocity" is used but this is incorrect as the quantity is a scalar.
The large impedance contrast between air and water (the ratio is about 3600) and the scale of surface roughness means that the sea surface behaves as an almost perfect reflector of sound at frequencies below 1 kHz. Sound speed in water exceeds that in air by a factor of 4.4 and the density ratio is about 820.
Absorption of sound
Absorption of low frequency sound is weak. The main cause of sound attenuation in fresh water, and at high frequency in sea water (above 100 kHz) is viscosity. Important additional contributions at lower frequency in seawater are associated with the ionic relaxation of boric acid (up to c. 10 kHz) and magnesium sulfate (up to c. 100 kHz).
Sound may be absorbed by losses at the fluid boundaries. Near the surface of the sea losses can occur in a bubble layer or in ice, while at the bottom sound can penetrate into the sediment and be absorbed.
Sound Reflection and Scattering
Boundary interactions
Both the water surface and bottom are reflecting and scattering boundaries.
Surface
For many purposes the sea-air surface can be thought of as a perfect reflector. The impedance contrast is so great that little energy is able to cross this boundary. Acoustic pressure waves reflected from the sea surface experience a reversal in phase, often stated as either a “pi phase change” or a “180 deg phase change”. This is represented mathematically by assigning a reflection coefficient of minus 1 instead of plus one to the sea surface.
At high frequency (above about 1 kHz) or when the sea is rough, some of the incident sound is scattered, and this is taken into account by assigning a reflection coefficient whose magnitude is less than one. For example, close to normal incidence, the reflection coefficient becomes
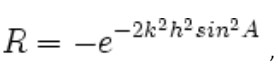
where h is the rms wave height.
A further complication is the presence of wind generated bubbles or fish close to the sea surface. The bubbles can also form plumes that absorb some of the incident and scattered sound, and scatter some of the sound themselves.
Seabed
The acoustic impedance mismatch between water and the bottom is generally much less than at the surface and is more complex. It depends on the bottom material types and depth of the layers. Theories have been developed for predicting the sound propagation in the bottom in this case, for example by Biot and by Buckingham
At Target
The reflection of sound at a target whose dimensions are large compared with the acoustic wavelength depends on its size and shape as well as the impedance of the target relative to that of water. Formulae have been developed for the target strength of various simple shapes as a function of angle of sound incidence. More complex shapes may be approximated by combining these simple ones.
Propagation of sound
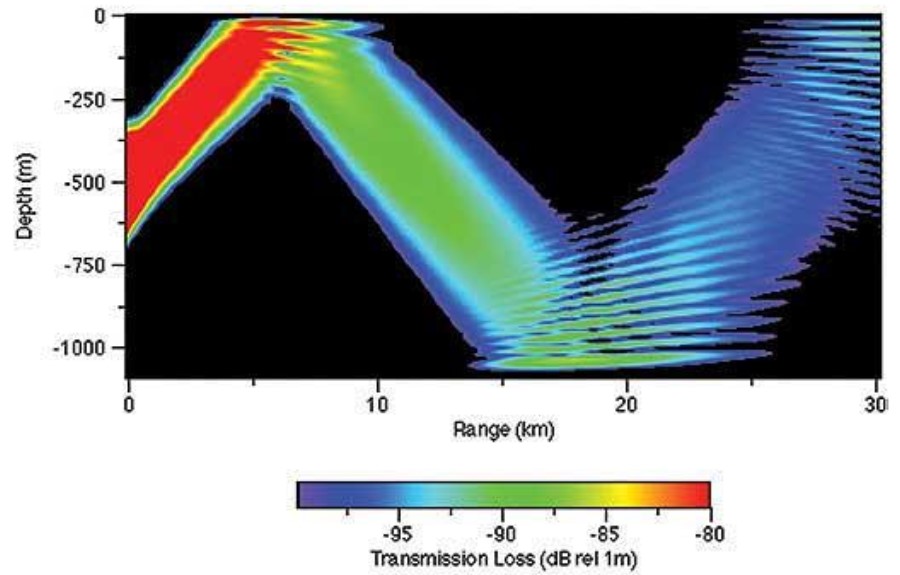
Underwater acoustic propagation depends on many factors. The direction of sound propagation is determined by the sound speed gradients in the water. In the sea the vertical gradients are generally much larger than the horizontal ones. These facts, combined with a tendency for increasing sound speed with increasing depth due to the increasing pressure in the deep sea reverses the sound speed gradient in the thermo cline creating an efficient waveguide at the depth corresponding to the minimum sound speed. The sound speed profile may cause regions of low sound intensity called "Shadow Zones" and regions of high intensity called "Caustics". These may be found by ray tracing methods.
At equatorial and temperate latitudes in the ocean the surface temperature is high enough to reverse the pressure effect, such that a sound speed minimum occurs at depth of a few hundred metres. The presence of this minimum creates a special channel known as Deep Sound Channel, previously known as the SOFAR (sound fixing and ranging) channel, permitting guided propagation of underwater sound for thousands of kilometres without interaction with the sea surface or the seabed. Another phenomenon in the deep sea is the formation of sound focussing areas known as Convergence Zones. In this case sound is refracted downward from a nearsurface source and then back up again. The horizontal distance from the source at which this occurs depends on the positive and negative sound speed gradients. A surface duct can also occur in both deep and moderately shallow water when there is upward refraction, for example due to cold surface temperatures. Propagation is by repeated sound bounces off the surface.
In general, as sound propagates underwater there is a reduction in the sound intensity over increasing ranges, though in some circumstances a gain can be obtained due to focussing. Propagation loss (sometimes referred to as transmission loss) is a quantitative measure of the reduction in sound intensity between two points, normally the sound source and a distant receiver. If Is is the far field intensity of the source referred to a point 1 m from its acoustic centre and Ir is the intensity at the receiver, then the propagation loss is given by
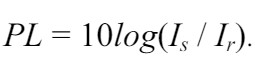
In this equation Ir is not the true acoustic intensity at the receiver, which is a vector quantity, but a scalar equal to the equivalent plane wave intensity (EPWI) of the sound field. The EPWI is defined as the magnitude of the intensity of a plane wave of the same RMS pressure as the true acoustic field. At short range the propagation loss is dominated by spreading while at long range it is dominated by absorption and/or scattering losses.
An alternative definition is possible in terms of pressure instead of intensity, giving
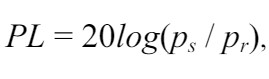
where ps is the RMS acoustic pressure in the far-field of the projector, scaled to a standard distance of 1 m, and pr is the RMS pressure at the receiver position.
These two definitions are not exactly equivalent because the characteristic impedance at the receiver may be different from that at the source. Because of this, the use of the intensity definition leads to a different sonar equation to the definition based on a pressure ratio.[14] If the source and receiver are both in water, the difference is small.